重力場というのは、重ね合わせ可能な場であると考えられています。例えば、同じ大きさで同じ質量の惑星A,Bがあるとします。この２つの惑星のちょうど中間にある場所Pの重力はゼロになります。これは、場所Pへ及ぶ惑星Aからの重力と惑星Bからの重力を加えるゼロになるという重ね合わせの法則を用いて説明されるものです。コマによる回転重力場は確実に存在し、地球重力場の勢力範囲内でコマを回すと、コマの周りには、地球の重力場とコマの回転重力場が存在することになります。重力場は重ね合わせ可能な場なのですから、この２つの重力場は当然重ね合わせられると考えねばなりません。
場を重ね合わせるとどうなるかは、「1.4 野球のカーブボールは何故曲がるのか」で考えたように、およその想像はつくでしょう。コマが歳差運動するのは、野球のカーブボールが曲がる理由と同じようなことです。コマの回転軸を地球重力と平行に回転させると安定して回転するのは、回転している弾丸がよりまっすぐ飛ぶということと同じようなことです。
ただし、空気の流れのような流体は、より増幅された方向へ力が働くのに対し、重力の場合は、その反対方向に力が働きます。(図1.3)
重力というものは、物体を加速させる能力を持っていることはよく知られています。リンゴが木から落ちるのは、重力によって引っ張られるからです。リンゴが落ちる方向は、正確に地球の中心に向かっています。それは、重力の方向に一致して物体は加速されるからです。図1.1のコマが台を中心に回転運動することに注意してください。コマは重ね合わされた重力場の方向にしたがって運動します。このコマの周りの局所的な重力場の方向は上から下ではなくなっているのです。コマは、多くの人々が思い込んでいる「重力の方向は上から下である」ということを変化させる能力を持っているのです。
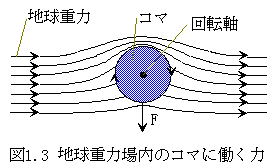
コマは、地球などの周りの重力場の方向を変化させる能力があることはわかりましたが、次には、地球などの外部の重力場がない場所で、自力で一定の方向へ推進力を発揮させる方法を考えることにしましょう。
これについても、流体の類推から始めることにしましょう。野球のカーブボールが曲がるのは、流体の局所的な圧力差を利用したものですが、このような流体的な揚力を応用して、推進力を発揮させる方法はあるのでしょうか。もちろんプロペラは使ってはいけません。プロペラは、空気を押すことによる反動（反作用）を応用しているものですから、揚力ではありません。
わかりましたか。[解答]
- ヒント１；飛行機の翼
- ヒント２；ブーメラン
- ヒント３；フリスビー
redsky@graveng.jp
1.7 重力推進機関の原理
サブメニューに戻る
ホームページに戻る