車に乗っていて、加速すると体がシートに押しつけられるのを感じます。このような力は見かけの力とよばれ、遠心力やコリオリの力などもこの力であると言われています。この力が見かけとよばれる理由は、座標の取り方によって現れるものであり、実在しないという点で見かけとよばれるようです。力に見かけがあるならば、実在の力もなくてはなりません。実在の力とは何でしょうか。例えば糸を引っ張る力が実在の力であるとも言われます。ならば、玉に糸をつけてぐるぐる回せば糸の張力は実在の力になります。しかし、この力は遠心力でもありました。遠心力が見かけの力なら、この糸の張力も見かけの力であると見なさなければならないことになります。
結局、見かけの力と実在の力との違いは現代物理学においても明確にされているわけではないと結論せざるを得ません。この見かけの力と実在の力の違いということは物理学の根幹に関わる重要なテーマであり、決して侮れるものではありません。例えば、誰かに殴られたとした場合、その力が見かけの力であれば、殴った人に罪はありませんが、実在の力であれば、傷害罪になります。裁判官が参考人に物理学者をよび、「その力は実在の力ですか、それとも見かけの力ですか」と質問したとき、物理学者はどう答えればよいのでしょうか。その答えをこれから見出すことにしましょう。
見かけの力とは何なのでしょうか。物理学では次のように説明されています。
「慣性系に対し、加速度aをもつ座標系があるとき、この座標系でニュートンの運動方程式を立てる際に加速度aの効果を取り入れるため付加すべき力。この力は座標変換に伴って導入するべきもので、物体に作用する実在の外力ではないため見かけの力とよばれる。この力は慣性力ともよばれ、コリオリの力、遠心力はこの力の一種である。」この説明では、実在の力のことを「物体に作用する実在の力」と言っています。このことから逆に見かけの力とはこの実在の力ではないものということになります。それでは遠心力は物体に作用しない力ということになりますが、そのようなことは決してありません。遠心力も物体に作用しているからこそ、遠心分離器なる発明品があるのです。ここで挙げた見かけの力の説明は内部矛盾を含んでおり、正しい命題とは言えないものです。この理由は見かけの力とよぶものと実在の力とよぶものの認識の曖昧さと混同によって生じていると考えられます。
この命題が誤りであることは明らかですが、前半の部分は何か意味がある文章のようなので、とりあえず、見かけの力とは、
「慣性系に対し、加速度aをもつ座標系があるとき、この座標系でニュートンの運動方程式を立てる際に加速度aの効果を取り入れるため付加すべき力」と解釈しておくことにしましょう。
力に見かけがあるなら、速度にも見かけがあるに違いありません。力とは速度の時間的変化の関数であると見なすことができ、問題とする質量が一定なら、力は速度の従属関数であると考えられるからです。とりあえず解釈した命題と同じように速度について書けば、見かけの速度とは、
「慣性系に対し、速度vをもつ座標系があるとき、この座標系でニュートンの運動方程式（運動量の方程式）を立てる際に速度vの効果を取り入れるため付加すべき速度」ということになるでしょう。力ではよくわからなかったことも、速度についてはわかりそうです。おそらく、この意味は走っている列車から見て駅は列車の速度と反対方向へ運動していると考えることができるといったことで、このように考えることは当然可能です。この際、問題となる速度はいわゆる相対速度とよばれる概念と同一のものであると考えられます。このことから、物理学において使われてきた見かけという言葉の意味は相対という意味に置き換えることが可能であると考えられます。
見かけという言葉の意味は相対という意味に置き換えることが可能であると考えて、今まで使われてきた物理用語を再定義することにしましょう。
見かけの速度 ； 相対速度このように解釈すれば、見かけの力という意味が明確になります。例えば、加速している列車から見ると駅は反対方向へ相対加速度を持ち、列車を基準にした座標系からは、あたかも、駅にはその相対加速度に見合う力が働いているかのように観測されることになります。しかしながら、相対加速度を用いた力である相対力では、いかなる物体も実際に押す事はできません。今まで使われていた見かけの力の概念には、実在の力も含まれており、ここではっきり見かけの力から実在の力を除外したものを相対力とよび定義することにしましょう。
見かけの運動量 ； 相対運動量 ＝ 質量 × 相対速度
見かけの加速度 ； 相対加速度 ＝ 相対速度の時間微分
見かけの力 ； 相対力 ＝ 質量 × 相対加速度
それでは、実在の力とは何でしょうか。われわれは2.2 絶対的な速度で非相対の速度を慣性速度と名付けたのでした。相対速度が見かけの速度なら、非相対速度が実在の速度になるのでしょう。ニュートンの運動方程式は、この実在の力を反映しているものと考えられ、その記述方法に従えば、実在の力＝質量×実在の速度の時間微分ということになるでしょう。このような対応を考慮し、関連する用語を再定義することにしましょう。
実在の速度 ； 慣性速度この中の「慣性力」という用語は、今までは、何か見かけの力の一種あるいはそれ自身として扱われていました。そのような曖昧な概念と、ここで再定義された「慣性力」はまったく異なるものです。できれば混同を避けるために、「慣性力」という用語を新たな物理的意味を持つ用語として使いたくはありませんが、このよび方は、この力の意味を簡潔に示すのに最も適当であると考えられるので、このようにわれわれはよぶことにしましょう。従来、使われてきた「慣性力」という言葉の意味は加速される自動車に乗っていてシートに押しつけられるような見かけの力ということですが、この力は実際は見かけではなく、実在の力なので、本質的には問題はありません。次に、これを証明しましょう。
実在の運動量 ； 慣性運動量 ＝ 質量 × 慣性速度
実在の加速度 ； 慣性加速度 ＝ 慣性速度の時間微分
実在の力 ； 慣性力 ＝ 質量 × 慣性加速度
いま宇宙空間にエレベータが浮かんでいるものとします。外部からの重力などの外力はいっさいないものとし、このエレベータの内部は慣性座標系であるものと見なすことができ、エレベータの中央にはリンゴが浮かんでおり、この時点でエレベータとリンゴの相対速度はゼロとし、リンゴはエレベータに対して静止しているとしましょう。
エレベータを非重力の力を使い引っ張れば、エレベータから見てリンゴには力が働いているように見えます。これは、エレベータとリンゴの間の相対加速度によって生ずる相対力であり、いわゆる「見かけの力」です。
リンゴはやがてエレベータの壁にぶつかることになります。このとき、リンゴと壁の間には力が生じ、この力は加速する車に乗った人がシートに押しつけられる力と同じ種類のものです。この力は相対力である「見かけの力」でしょうか。この力が相対力であるとすれば、２つの玉がぶつかって、はじき飛ばされるときの相互作用も相対力である「見かけの力」であると認めなければならなくなります。
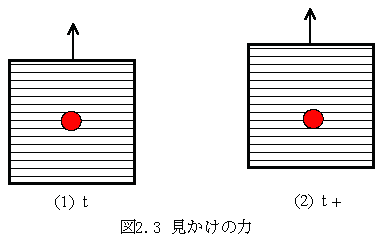
本来、この思考実験のリンゴは何もエレベータの内部にある必要はなく、外部にあっても結果は同じで、ただ２つの物体の衝突の現象にすぎないものです。赤玉、青玉があるとし、赤玉が加速しながら静止している青玉にぶつかる、といった現象と本質的に何等変わりがありません。赤玉が青玉にぶつかる前は、赤玉からみて青玉には相対加速度に見合う力が働いているように見えます。やがて、赤玉が青玉にぶつかったとき、赤玉は青玉を押し、青玉は反作用で赤玉を押し返します。青玉の反作用で赤玉を押し返す力は加速している車に乗った人がシートに押しつけられる力と同じ種類のものであることは明らかです。車に乗った人がシートに押しつけられる力は、普通の意味での力と何等区別する必要はなく、このような力は実在の力であると考えられます。青玉が赤玉にぶつかる前とぶつかった後の違いは、青玉が実際に動いたか動いていないかの違いがあり、別の言い方をすれば、慣性速度が変化したかしないかの違いがあるのです。あるいは、青玉にはエネルギーが加えられたか加えられなかったかの違いがあるのです。
いままで一般に考えられていた「見かけの力」なる概念は、この違いを認識しておらず、相対力と実在の力を混同していたものです。見かけの力は慣性速度を変化させないかエネルギーを加えられない力で、実在の力は慣性速度を変化させるかエネルギーを加えられる力なのです。
ところで、静止している物体に力を加えるとき、その力は見かけの力なのでしょうか、それとも実在の力なのでしょうか。その物体は動いていないのですから、慣性速度は変化しないように見えます。また、一般的な物理学の知識では、仕事（エネルギー）＝力×変位と定義されているので、力を加えても物体が動かなければ、エネルギーは必要ないと考えられています。それならば、その力は見かけなのでしょうか。この変位という量が速度と関係していることは明らかです。このことは、ある座標系から観測すれば、物体は動かないが、他の座標系から観測すれば、物体は動いているということが起こります。力とエネルギーの関係についても考え直してみる必要があるようです。ようやく、力とエネルギーの関係について考えるときがやってきたようです。
redsky@graveng.jp
2.4 力とエネルギー
サブメニューに戻る
ホームページに戻る